《平面 生命之花 7圆灵 与 立体 生命之球 13球灵 36重大罗天 柏拉图立体 欧拉定理 欧拉公式 足球》

7圆灵 平面：

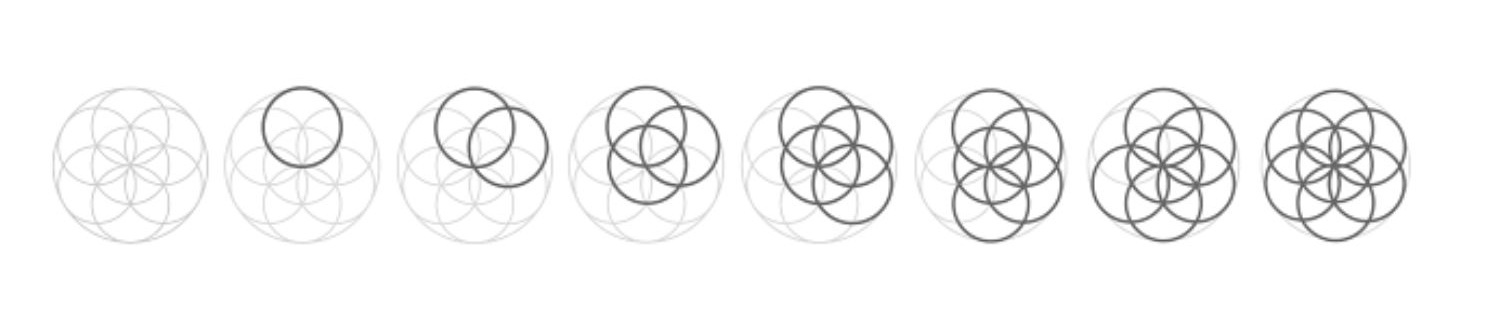
1个圆 空虚 寂寞 无聊，交合 1个圆 有趣，联合 1个圆 稳固，4个圆 和谐，5个圆 完美，95至尊 95+=14+=5 （正多面体 正五边形 最多5边形，组成正12面体。完美。），6个圆 不稳定 空虚，立即 成为 7个圆，完美贴合，完美结合，完美交合，满足。星期日，休息。

13球灵 立体：

生命之球 金丹是完美的。球是完美的。浑润之完美球。可以 与 6个 球 完美 平行 贴合。无法 与 其他 6个 球 完美 贴合。 平行 的 7个球 完全 贴合，两边 各 3个球，不互相 完全 贴合。有 活动 空隙，活动 空间。因此 没有 完全 稳固 不动 的 完美 的 终极 的 等完美球 贴合体。

总有 误差 缺憾。但整体 却是 完美的。

只能在1个球周围精密放置6个球。这6个球 必然 在 一个 平面上。已经无法移动。一向上 缩，就放不下 6个球了。

第二层 只能 放 3个球，但3个球 每个球的球心 在 下面 3个球 的 中心，而非 2个球的中心。 那这3个球必然无法 相贴。那就 不存在 其他 球 相贴 的 可能。

因此，无法 在 空间中 贴近 更多球。最多 贴近 6+3+3颗球=12颗球。上下 是 2个 很小 的 空隙。

因此，一颗 完美 球，附近 最多 贴合 12颗 相同大小的 完美球。最多 只能 紧密 贴合 6颗。其他 6颗 无法 紧密 贴合。

因此，最多，可以 近似 理解为 贴合 ≈12.3456789随机（123456789）不循环无限长小数 颗。

1+12 不完美 立体 空间 贴合球灵 6个完美 6个 有 活动 间隙。1+6 完美 平行 空间 贴合球灵。

共 4圈。每圈 6颗。共 12 颗。

总结：

1个接近完全完美球金丹。

1+4：完美 相互交合。10000=16。

1+6：完美 平行贴合。平行 空间。

1+6 +6=13：完美 6平行贴合 绝对平行 空间。不完美 6贴合。

美国 国徽 13星。六芒星（两个三角形）中间还有一星，平均分布。

三十六重天外天 至高天 大罗天：

平面上 5排台球 可以 摆 15个台球。第二层10个，相互之间不贴合。第三层 6个，相互之间 更不贴合。第四层 3个，相互之间 更更不贴合。第五层 1个。共 35个 33层天 弥罗天 天宫 天堂。最高层 36 重天 大罗天。

元始天尊在大罗天，灵宝天尊在太清境大赤天，太上老君在太清境大赤天。

元始天尊，作为道教三清之首，居住在道教宇宙观中的最高层次——大罗天。大罗天被视为是至高无上的天界，象征着无限的广阔和神圣。元始天尊在此居住，体现了其在道教中的至高地位和对宇宙起源的深远影响。

灵宝天尊，居住在太清境大赤天。太清境大赤天位于三十三天之上。

玉清境清微天、上清境禹余天

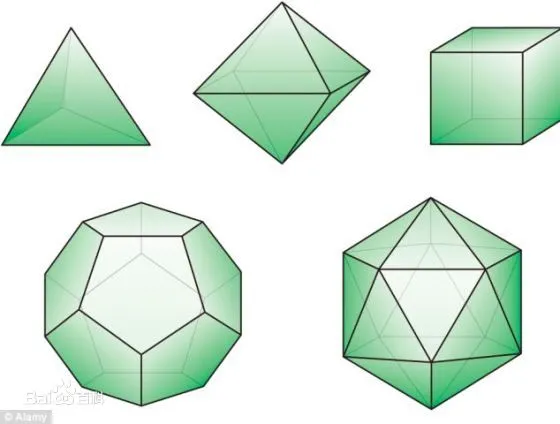
柏拉图立体：

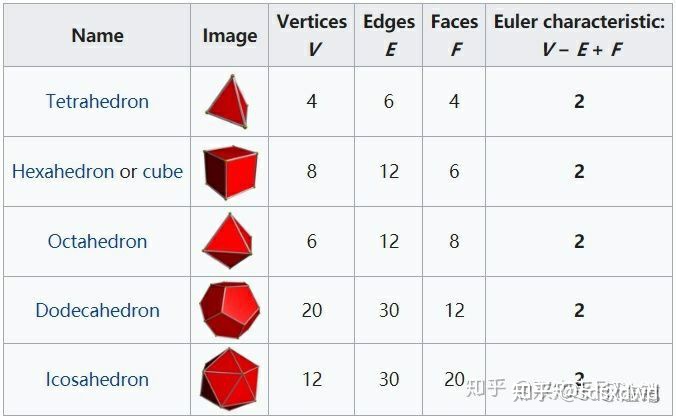
正4面体 4*3边形、正6面体 6*4边形、正8面体 8*3边形、正12面体 12*5边形、正20面体 20*3边形。正多面体。

星形四面体，两个四面体 叠加。8个尖。

六边形 可以 统一 完美 拼接 平面。完美二维数字。

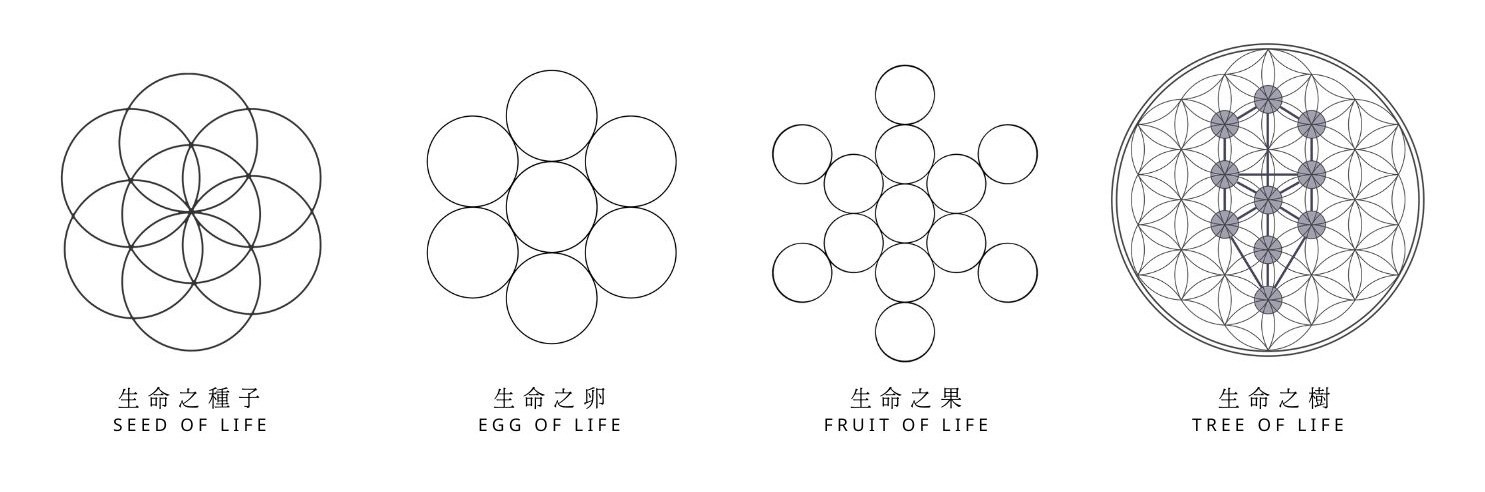
生命之种 生命之花 生命之卵 生命之蛋 生命之果 生命之树 梅塔特隆立方体 神圣几何

【解析生命之花】

生命之花：

古埃及神秘学派的核心，是一个无所不包的几何符号：生命之花（Flower of Life）。

生命之花是将圆形拆成许多全等的尖椭圆光轮而成。

过程重复7次，同时向外旋转，创造出“细胞”图案。

而每到第8次分裂就是一次新的向外旋转，如此重复下去，直到无限次，创造出母体。

虽然生命之花图样在二维看起来是一连串的圆形，

但其实是在表达三维空间球内有球的过程，

因此图样很像人体细胞的减数分裂，

也让生命之花成为自然创生过程的几何象征。

由于每个“细胞”都包含母体的模式，

生命之花就好比全像图片，和宇宙相仿，

其图样的树枝状结构描绘了光的几何互动模式，

如同人体内的遗传物质、DNA的遗传密码排列。

【生命之花与神圣几何】

a 象征“创世”，即对应《圣经》创世纪里的创世七天，

在神的“歇息日”完成了7个圆的“细胞”b 。

接着，“生命种子” c 出现，其中包含“生命之树” d 。

之后，“生命之卵” e 生成，也可以将图案简化成 f 。

下个阶段，诞生了“生命之花” g ，可以简化成1个中央圆和6个外接圆。

麦田圈中的神圣几何学

当“生命之花” i 中包含1个中央圆和12个外接圆时，即形成“生命之果” j 。

通过球心的直线可以标出5套信息体系，

将圆形生命之花的女性新生力量和和直线的男性法则整合起来，

结果就形成各种立体结构。

其中,“柏拉图立体”k 是形成物质世界的最基本的键结模式；

而“梅塔特隆立方体（Metraton's Cube）”l 被认为是一个神圣的浮雕，经常在一个物体或人周围而出，去挡住魔鬼和邪恶的力量。

梅塔特隆的拉丁名字是“梅塔特”—— 即一个引路人或者测量器，就像“创作物的几何学”。

古埃及人对神圣几何有多重视？

在他们眼中，神圣几何是数学的前提，是物理法则的基础，甚至是物质世界背后的形态发生结构。

神圣几何是宇宙密码，这套哲学起源自埃及的学习与度量神“透特（Thoth)”，

他“赐予秘密给古代哲学家和祭司，这些秘密保存在神话和传奇里流传至今。

所有寓意和象征符号都暗藏了灵性、心智、道德和物理的新生法则。

用拓扑学方法证明

尝试一下用拓扑学方法证明关于多面体的面、棱、顶点数的欧拉公式。

欧拉公式：

对于任意多面体（即各面都是平面多边形并且没有洞的立体），

假设F，E和V分别表示面，棱（或边），角（或顶）的个数，那末

F-E+V=2。

证明 如图（图是立方体，但证明是一般的，是“拓朴”的）：

1．把多面体（图中①）看成表面是薄橡皮的中空立体。

2．去掉多面体的一个面，就可以完全拉开铺在平面上而得到一个平面中的直线形，像图中②的样子。假设F′，E′和V′分别表示这个平面图形的（简单）多边形、边和顶点的个数，只需证明F′-E′+V′=1。

3．对于这个平面图形，进行三角形分割，也就是说，对于还不是三角形的多边形陆续引进对角线，一直到成为一些三角形为止，像图中③的样子。每引进一条对角线，F′和E′各增加1，而V′却不变，所以F′-E′+V′不变。因此当完全分割成三角形的时候，F′-E′+V′的值仍然没有变。有些三角形有一边或两边在平面图形的边界上。

4．如果某一个三角形有一边在边界上，例如图④中的△ABC，去掉这个三角形的不属于其他三角形的边，即AC，这样也就去掉了△ABC。这样F′和E′各减去1而V′不变，所以F′-E′+V′也没有变。

5．如果某一个三角形有二边在边界上，例如图⑤中的△DEF，去掉这个三角形的不属于其他三角形的边，即DF和EF，这样就去掉△DEF。这样F′减去1，E′减去2，V′减去1，因此F′-E′+V′仍没有变。

6．这样继续进行，直到只剩下一个三角形为止，像图中⑥的样子。这时F′=1，E′=3，V′=3，因此F′-E′+V′=1-3+3=1。

7．因为原来图形是连在一起的，中间引进的各种变化也不破坏这事实，因此最后图形还是连在一起的，所以最后不会是分散在向外的几个三角形，像图中⑦那样。

8．如果最后是像图中⑧的样子，可以去掉其中的一个三角形，也就是去掉1个三角形，3个边和2个顶点。因此F′-E′+V′仍然没有变。

即F′-E′+V′=1

成立，于是欧拉公式：F-E+V=2 得证。

公式应用

例：足球表面由五边形和六边形的皮革拼成，计算一共有多少个这样的五边形和六边形

答：足球是多面体，满足欧拉公式F－E+V=2，其中F,E,V分别表示面，棱，顶点的个数

设足球表面正五边形(黑皮子)和正六边形(白皮子)的面各有x个和y个，那么

面数F=x+y

棱数E=(5x+6y)/2（每条棱由两块皮子共用）

顶点数V=(5x+6y)/3（每个顶点由三块皮子共用）

由欧拉公式，x+y－(5x+6y)/2+(5x+6y)/3=2，

解得x=12。

所以，共有12块黑皮子

所以，黑皮子一共有12×5=60条棱，这60条棱都是与白皮子缝合在一起的

对于白皮子来说：每块白色皮子的6条边中，有3条边与黑色皮子的边缝在一起，另3条边则与其它白色皮子的边缝在一起。

所以白皮子所有边的一半是与黑皮子缝合在一起的，

那么白皮子就应该一共有60×2=120条边，120÷6=20。

所以共有20块白皮子。

或者，每一个六边形的六条边都与其它的三个六边形的三条边和三个五边形的三条边连接；每一个五边形的五条边都与其它的五个六边形的五条边连接

所以，五边形的个数x=3y/5。

之前求得x=12，所以y=20。

对于任意一个多面体P，有V个顶点，E条边，F个面，定义,为所有面的最小边数。可以得到。

任意一个面至少由3条边围成，所以显然成立。

柏拉图形状 柏拉图立体：

正多面体：正4面体 4*3边形、正6面体 6*4边形、正8面体 8*3边形、正12面体 12*5边形、正20面体 20*3边形。

星形四面体，两个四面体 叠加。8个尖。

多边形：三角形。最少3个顶点 3个角 3条边。三角形具有稳定性。

多面体：

四面体。面最少的体。正四面体（面最少的正多面体）。最少4个顶点 4个角落 4个3边形面 6（3×2）条边。

5个顶点，6面体。相当于2个四面体 共用一个面。一共6（4×2-2）个3角形面 3边形面。

8个顶点，正六面体 立方体（8个顶点，8个角落，6个4边形面，12条边。）

正五边形，正六边形，可以组合成 多面球体。

正多面体只能有五种（中间 1个球，交叉围绕4个球。共5个球），

用正三角形（正三边形）做面的正四面体、

正八面体（八面玲珑），

用正方形（正四边形）做面的正六面体（正方体），

用正五边形做面的正十二面体。

所谓正多面体，当然要首先保证它是一个多面体，而它的特殊之处就在于它的每一个面都是正多边形，而且各个面的正多边形都是全等的。

将正多面体的各个面剪下来，它们可以完全重合。

虽然多面体的家族很庞大，可是正多面体的成员却很少，仅有五个。

正多面体除正四面体外过任顶点和正多面体中心的直线必然经过正多面体的另一顶点，

并且这两个顶点到正多面体中心的距离都相等。

除正四面体外，正多面体的对棱、对面都平行。

欧拉定理：

F，E和V分别表示面，棱（或边），角（或顶）的个数，那么

F-E+V=2。

足球有32块皮子，最经典的一般用黑和白，12块五边形，20块六边形 。

可以用以下公示推导：

黑的是正五边形，白的是正六边形。

设黑皮x块,则白皮32－x块,顶点数V,棱数E,列方程：

5x+(32-x)*6=E*2 （每一条棱两块皮共用）

5x+(32-x)*6=V*3 （每一个顶点3块皮共用）

V+32-E=2 （欧拉公式）

解得x=12

所以黑皮的五边形为12块,白皮六边形为20块。

奥本海默 首个核爆球 外围 是由 6边形 和 5边形 块体 组合成 的。应该 类似 足球。